|
Страница 3 из 10 Самый древний из них гномон (рис. 1). В простейшем варианте он представляет собой вертикальный стержень, отбрасывающий тень на горизонтальную плоскость. Зная длину гномона L и измерив длину l отбрасываемой им тени, можно найти угловую высоту h Солнца над горизонтом по современной формуле: Древние использовали гномоны для измерения полуденной высоты Солнца в различные дни года, а главное в дни солнцестояний, когда эта высота достигает экстремальных значений. Пусть полуденная высота Солнца в день летнего солнцестояния равна Н, а в день зимнего солнцестояния h. Тогда угол ε между небесным экватором и эклиптикой равен 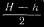 , а наклон плоскости небесного экватора к горизонту, равный 90° — φ, где φ — широта места наблюдения, вычисляется по формуле , а наклон плоскости небесного экватора к горизонту, равный 90° — φ, где φ — широта места наблюдения, вычисляется по формуле 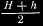 . С другой стороны, внимательно следя за длиной полуденной тени, можно достаточно точно подметить, когда она становится самой длинной или самой короткой, то есть иначе говоря, зафиксировать дни солнцестояний, а значит, и продолжительность года. Отсюда легко вычислить и даты солнцестояний. . С другой стороны, внимательно следя за длиной полуденной тени, можно достаточно точно подметить, когда она становится самой длинной или самой короткой, то есть иначе говоря, зафиксировать дни солнцестояний, а значит, и продолжительность года. Отсюда легко вычислить и даты солнцестояний.
|

